Bulk Modulus of Elasticity

What is Bulk Modulus

The bulk modulus of elasticity is a measure of how much a material resists changes in volume when pressure is applied. In other words, it’s a measure of a material’s stiffness or resistance to compression. This property is an important factor in engineering and physics, as it can tell us how materials will react when placed under pressure.

Diagram showing a cube decreasing in volume due to volumetric pressure — Change in volume due to compressive pressure

Definition & Explanation

The bulk modulus, denoted by the letter (B or K), is defined as the ratio between the (volumetric stress) and the relative change in volume (volumetric strain).

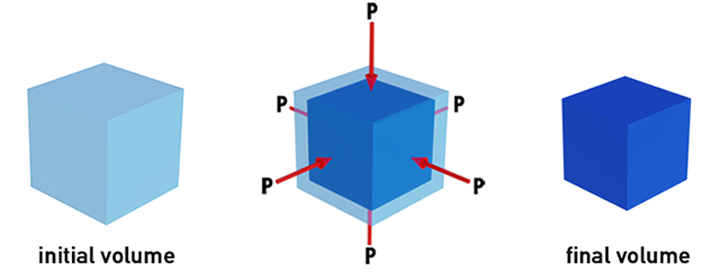
To explain the bulk modulus, let’s assume we had a container filled with water, and we placed a cube inside of it. The fluid is going to push on the cube’s surface in all directions, creating pressure on the cube. Due to all that compressing pressure, the cube’s volume will decrease. The ratio between the pressure and the relative change in volume is the bulk modulus.

Diagram of a water container with a cube inside of it

The higher the bulk modulus value (K), the higher the elasticity or stiffness of that material. In other words, it takes more force to compress it than a material with a lower bulk modulus value. Some materials have naturally high values for their bulk modulus; others require special treatments such as heat treatment or chemical hardening to increase their elasticity.

The bulk modulus, same as all the other elastic moduli, is only practical while the deformation is elastic, meaning that deformation is recoverable once the load / force is removed, and it is not permanent.

Formula & Units

Bulk modulus (K) = volumetric stress / volumetric strain

K = - \frac{Δ P}{(\frac{Δ V}{V_{o}})}

Where:

K is the bulk modulus of elasticity
ΔP is the change in applied pressure
ΔV is the change in volume
V_o is the original volume

The negative sign indicates that when pressure increases, the volume decreases.

The SI unit of bulk modulus is pascal (Pa), which is equal to 1 Newton per square meter (N/m²).

The US customary unit of bulk modulus is pounds per square inch (psi).

Bulk Modulus Example

Suppose you needed to know how much pressure is required to reduce the volume of a rubber material by 1%, you can easily do that by simply taking 1% of the Bulk modulus of rubber which is approximately (2 GPa).

So to reduce the rubber material volume by 1%, you would need to exert a pressure of

0.01 x 2 = 0.02 GPa

Bulk Modulus Calculation

Find the bulk modulus of a cube under a volumetric pressure of 15 N/m², and the volume change due to that pressure is -10 mm³. The side length of the cube is 100 mm.

Solution

Step 1) We write down the given parameters:

Δp = 15 N/m² ΔV = -10 mm³ L = 100 mm

Step 2) We need to find the volumetric strain:

\frac{Δ V}{V_{o}} = \frac{- 10^{3}}{100^{3}} = 0.001

Step 3) Now, we can find the bulk modulus of the cube:

K = \frac{15}{0.001} = 15, 000 N / m^{3}

Factors Affecting Bulk Modulus

The bulk modulus of a material can be affected by several factors, including:

Chemical composition and structure: The bulk modulus of a material is strongly dependent on its chemical composition and structure. Different materials have different bonding types, crystal structures, and densities, which can affect their bulk modulus.
Pressure: The bulk modulus of a material generally increases with increasing pressure. At higher pressures, materials become more difficult to compress, resulting in a higher bulk modulus.
Temperature: The bulk modulus of a material generally decreases with increasing temperature. At higher temperatures, materials tend to expand, leading to a lower bulk modulus.
State of matter: The bulk modulus of a material can also depend on its state, such as whether it is a solid, liquid, or gas. For example, the bulk modulus of a gas is significantly lower than that of a liquid or solid due to the greater distance between its molecules.

Applications of Bulk Modulus

Bulk Modulus has many practical applications across multiple industries including:

Hydraulic systems: Bulk modulus is crucial in the design and operation of hydraulic systems. The use of materials with high bulk modulus is beneficial in hydraulic systems as they facilitate efficient transmission of pressure changes.
Building and construction: Bulk modulus plays an important role in the design and construction of buildings and other structures. Materials such as concrete and steel with high bulk modulus are utilized to provide strength and stability to the structures.
Geology: Bulk modulus is used to study the properties of rocks and minerals under high pressures and temperatures. It is important in understanding the behavior of the Earth’s crust and mantle, as well as in the exploration and extraction of natural resources.
Acoustics: Bulk modulus is used in acoustics to calculate the speed of sound in different materials, which is important for designing acoustic systems and predicting their performance. By knowing the bulk modulus of different materials, engineers can design sound insulation materials that can block or absorb sound waves effectively.

Bulk Modulus Summary
Definition	The material’s resistance to the elastic change in volume when under a volumetric pressure
Symbol	B or K
Formula	$K = - \frac{Δ P}{(\frac{Δ V}{V_{o}})}$
Units	Si unit (Pa)	US unit (psi)

What factors affect the bulk modulus of a material?: The bulk modulus of a material is influenced by several factors, including the intermolecular bonding strength, density, and crystal structure of the material. Additionally, temperature and pressure can also impact the bulk modulus of a material.

Can bulk modulus be negative?: No, for the bulk modulus to be negative, the change in volume and pressure must both have the same sign (either positive or negative), which cannot happen, as a positive change in pressure or an increase in pressure will always decrease the volume.

What are Some Examples of Materials with High Bulk Moduli?: Materials with high bulk moduli include metals, rocks, ceramics, plastics, and rubbers. Metals usually have higher bulk moduli than other materials because their molecules are held together more tightly.

How can I calculate the Bulk Modulus of a particular material?: Bulk modulus can be calculated by measuring volume change under different pressures, either experimentally or theoretically using numerical methods like finite element analysis or computational fluid dynamics.
Alternatively, certain materials may have published Bulk modulus values determined from previous studies or experiments.