Flexural Modulus

What is Flexural Modulus

Flexural modulus, also known as the bending modulus or the modulus of elasticity in bending, is a mechanical property of a material that measures its stiffness or resistance to bending when a force is applied to it. The higher the flexural modulus, the more resistant the material is to bending.

Diagram showing the flexural or bending deformation in two rectangular beams

Flexural modulus is an important property in materials science and engineering, as it can be used to design objects that must bear weight or withstand pressure without being deformed, such as structural beams, bridges, and other structural components.

Flexural Modulus Test

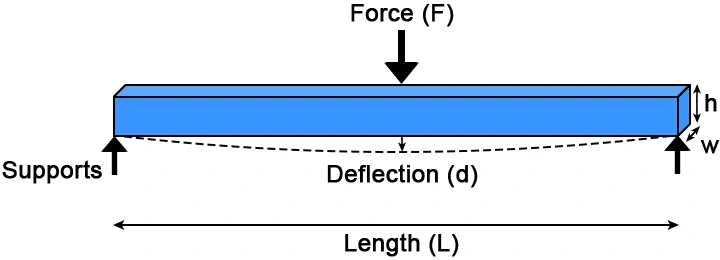
Diagram showing the flexural modulus three point test on a rectangular beam — Flexural modulus - three point test on a rectangular beam

The flexural modulus is typically measured using a test called the three-point bend test, in which a rectangular sample, with width (w), and height (h) is placed on two supports, with distance (L) between them. Once the sample is in place, a perpendicular force (F) is applied to the long edge of the sample, which creates a displacement in the material called deflection (d). Those parameters (w, h, L, F, and d) are used to calculate the flexural modulus in a material, as shown in the flexural modulus formula below.

Formula & Units

Flexural Modulus Formula (E_{f l e x}) = \frac{L^{3} \times F}{4 w h^{3} d}

Where:

L is the distance between the two supports
F is the perpendicular applied force
w is the width of the sample
h is the height of the sample
d is the deflection in the sample

The SI unit of flexural modulus is pascal (Pa), which is equal to 1 Newton per square meter (N/m²).

The US customary unit of flexural modulus is pounds per square inch (psi).

Factors Affecting Flexural Modulus

Having a good understanding of the factors that can influence the flexural modulus of a material is essential for choosing the appropriate material for a particular application and for predicting its behavior under different conditions. Some of the main factors that can affect the flexural modulus of a material are:

Material composition: The composition of a material, including the type and amount of filler materials, can affect its flexural modulus. For example, materials with a higher concentration of filler materials, such as glass fibers, tend to exhibit higher flexural moduli.
Temperature: Temperature can have a significant effect on the flexural modulus of materials, particularly in polymers and composites. As the temperature increases, the material becomes more flexible and the flexural modulus decreases.
Strain rate: The rate at which a material is subjected to bending stress or strain rate can affect its flexural modulus. Generally, higher strain rates tend to result in higher flexural moduli.
Manufacturing process: The flexural modulus of a material can be affected by the manufacturing process used to produce it. For instance, materials manufactured through molding or extrusion processes generally exhibit higher flexural moduli compared to those produced through casting.

Applications of Flexural Modulus

Flexural modulus plays a critical role in determining the suitability of materials for various applications. Some of the applications where the flexural modulus is particularly important are:

Construction: In the construction industry, materials with high flexural moduli are commonly used in structural applications, such as beams and columns, to ensure a particular material can support a certain amount of weight without failing or deforming beyond acceptable limits.
Automotive and Aerospace: The design and manufacture of components for the automotive and aerospace industries, such as suspension systems and wing structures, rely heavily on flexural modulus. Materials with high flexural moduli are favored in these applications because of their capacity to withstand deformation under load while maintaining their shape and structural integrity over time.
Medical Devices: Flexural modulus is also an important consideration in the design and manufacture of medical devices, such as implants and prosthetics. Materials with suitable flexural moduli are carefully selected to ensure that these devices can withstand the stresses and strains of the body and provide the necessary support and functionality.

Flexural Modulus Summary
Definition	The material’s tendency to resist bending deformation when a force is applied to it
Symbol	$E_{f l e x}$
Formula	$E_{f l e x} = \frac{L^{3} \times F}{4 w h^{3} d}$
Units	Si unit (Pa)	US unit (psi)

How is flexural modulus measured?: Flexural modulus is typically measured through a standardized bending test, such as the three-point or four-point bending test, which involves applying a load to a sample of the material in a specific manner and measuring the resulting deflection.

What does flexural modulus tell you?: Flexural modulus describes a material’s ability to resist bending deformation when a force is applied to it. So a higher flexural modulus means a material is pretty stiff in bending, and vice versa.

Is flexural modulus the same as young’s modulus?: In an ideal-homogeneous material, yes, the flexural and young’s moduli would be the same, however, most materials have different strengths in tensile vs compression, therefore having different values for flexural modulus and young’s modulus.

How is flexural modulus different from the other elastic moduli?: Flexural modulus measures a material’s resistance to bending. While other types of elastic moduli measure a material’s resistance to different types of deformation. For instance, Young’s modulus measures a material’s resistance to stretching or compression.

What factors can affect the flexural modulus of a material?: Several factors can affect the flexural modulus of a material, including its composition, temperature, strain rate, and manufacturing process.